Задачи
Всероссийского игрового конкурса
«Кит — компьютеры,
информатика, технологии»
Всероссийского игрового конкурса
«Кит — компьютеры,
информатика, технологии»
2009 год 10-11 классы. Задачи, оцениваемые в 3 балла.
1. При работе в интернете одна из страниц была отображена так, как показано на рисунке.
Это произошло из-за…
А) неправильных настроек разрешения экрана
Б) неправильных настроек монитора
В) неверного определения кодировки страницы
Г) ограничения провайдером доступа к этому сайту
Д) необходимости ввода пароля для просмотра этой страницы
2. Во сколько раз число 1111002 больше 2010?
А) в 2/3 раза
Б) в 2 раза
В) в 3 раза
Г) в 1,5 раза
Д) числа одинаковы
3. В группе детского сада для выхода на прогулку каждому из 2/3 мальчиков сопоставлена единственным образом в пару девочка, и каждая из 3/5 всех девочек образует единственную пару с мальчиком. Какая доля группы детей детского сада разбита на пары?
А) 2/3
Б) 3/5
В) 2/5
Г) 6/19
Д) 12/19
4. Какой цвет обозначает первая буква в цветовой модели CMYK?
А) Сhocolate (шоколадный)
Б) Сoral (коралловый)
В) Сrimson (малиновый)
Г) Сyan (голубой)
Д) Сhartreuse (зеленовато-желтый)
5. Какое сочетание клавиш в текстовом редакторе Notepad позволяет переместить курсор в конец документа?
А) Ctrl + End
Б) End
В) Ctrl + Del
Г) Shift + Del
Д) Alt + Home
6. Какое наименьшее количество точек необходимо удалить из фигуры, чтобы никакие четыре из оставшихся не являлись вершинами какого-нибудь квадрата?А) 1
Б) 2
В) 3
Г) 4
Д) 0
7. Какое из слов НЕ является названием языка программирования?
А) Visual Studio
Б) PHP
В) Pascal
Г) Java
Д) Python
8. Продавец продает шапку по цене 400 рублей. Подходит покупатель, но у него есть только купюра достоинством 500 рублей. У продавца нет сдачи, и он разменивает у соседки эту купюру на пять купюр достоинством по 100 рублей. Продавец отдает покупателю шапку и сдачу в 100 рублей. Через какое-то время приходит соседка и говорит, что 500 рублей фальшивые, требует отдать ей деньги. Продавец возвращает ей деньги. На сколько рублей обманули продавца?
А) 100
Б) 400
В) 500
Г) 900
Д) 1000
9. Дана таблица:
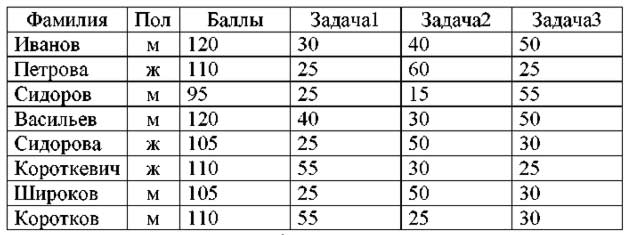
Какое количество записей таблицы удовлетворяет запросу: ((Пол=м) и (Баллы>105)) или (Задача1+Задача3<Задача2)
А) 6
Б) 7
В) 8
Г) 4
Д) 5
10. Plug&Play(включил и играй) – это…
А) компьютерная программа, моделирующая технологию музыкального проигрывателя
Б) компьютерная игра
В) компьютерная приставка с джойстиком
Г) компьютерная программа, использующаяся исключительно для поиска музыки и фильмов в Internet
Д) технология, предназначенная для быстрого определения и конфигурирования устройств
2009 год 10-11 классы. Задачи, оцениваемые в 4 балла.
11. Покажем процедуру построения снежинки Коха, которая является примером фрактала. Шаг построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми той же длины, как показано на рисунке. Граница снежинки Коха – предельное положение кривой после выполнения бесконечного числа шагов. Какова длина границы снежинки Коха, если начальный треугольник имел стороны 1?
А) 3
Б) 4/3
В) 2π(греческая пи)
Г) 2π(греческая пи)/3
Д) бесконечна
12. Выберите правильный результат логической операции: 00101011 & 10101001
А) 10101011
Б) 00101001
В) 01111100
Г) 11010110
Д) 01010100
13. Решите уравнение 11х + 20y= 15х+y .
А) x = 3, y = 3
Б) x = 3, y = 4
В) x = 4, y = 2
Г) решений нет
Д) решений бесконечно много
14. «С++» – это…
А) строго типизированный компилируемый язык программирования
Б) строго типизированный интерпретируемый язык программирования
В) язык и система логического программирования, основанные на языке предикатов математической логики дизъюнктов Хорна, представляющей собой подмножество логики предикатов первого порядка
Г) распространённый искусственный язык, созданный в 1887 году и призванный служить универсальным международным языком между людьми
Д) адаптированная международная система единиц, современный вариант метрической системы Си
15. На вопрос: "Кто из трех учащихся изучал математическую логику?" – получен верный ответ: "Если изучал первый, то изучал и третий, но неверно, что если изучал второй, то изучал и третий". Кто изучал математическую логику?
А) 1
Б) 2
В) 3
Г) 1 и 3
Д) 1, 2 и 3
16. При Интернет-соединении с максимальной скоростью скачивания 192 килобит/c аудио-файл размером 3600 килобайт будет в лучшем случае скачиваться…
А) 5 минут
Б) больше 15 минут
В) 10 минут
Г) 2,5 минуты
Д) меньше 30 секунд
17. Операционная система Linux имеет архитектуру …
А) модульного ядра
Б) монолитного ядра
В) микроядра
Г) экзоядра
Д) наноядра
18. Из точки А с координатами (0, 0) необходимо построить лесенку из трёх ступенек в точку В с координатами (5, 3). Каждая ступенька должна иметь одну единицу по высоте и целое количество единиц в длину. Сколько всего можно построить таких лесенок, если известно, что первая ступенька должна начинаться в точке А?
А) 4
Б) 5
В) 6
Г) 7
Д) 10
19. В таблице 5x5 расставили числа от 1 до 25 так, что в каждой строке и каждом столбце числа упорядочены по возрастанию. При этом наименьшее значение суммы чисел по периметру таблицы, которое могло получиться, равно…
А) 208
Б) 190
В) 200
Г) 212
Д) 186
20. Дан фрагмент электронной таблицы:
Чему будет равно значение в ячейке D1, если в нее скопировать формулу из ячейки C1?
А) 80
Б) 70
В) 100
Г) 50
Д) 110
2009 год 10-11 классы. Задачи, оцениваемые в 5 баллов.
21. Была отсканирована фотография 5 см x 6 см. Настройки сеанса сканирования были установлены:
разрешение - 400 dpi;
глубина цвета - 24 bpp;
без сжатия.
Сколько байт потребуется для хранения данного изображения?
разрешение - 400 dpi;
глубина цвета - 24 bpp;
без сжатия.
Сколько байт потребуется для хранения данного изображения?
А) 2 232 004
Б) 12024
В) 115 200 000
Г) 454
Д) 38 400 000
22. Логическое выражение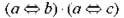 
эквивалентно…
эквивалентно…
23. Ваш приятель Дима живет в доме, в котором 8 квартир. Вы не знаете, в какой именно. Подойдя к дому, вы встречаете Славу, который знает, в какой квартире живет Дима, но на все вопросы он отвечает односложными «да» или «нет». Каково наименьшее количество вопросов, которое необходимо задать, чтобы определить квартиру Димы, при условии, что вы сначала задаете все свои вопросы, и только потом Слава выдает последовательность своих ответов (по порядку задаваемых вопросов)?
А) 1
Б) 2
В) 3
Г) 7
Д) 8
24. Два одноклассника решили пообщаться в сети между 10 и 11 часами и договорились ждать друг друга не более 30 минут. Но вот беда, точного времени встречи оговорено не было. Тогда каждый из них решил случайным образом выбрать время выхода в сеть между 10 и 11 часами. Какова вероятность того, что общение состоится?
А) 1
Б) 1/2
В) 1/3
Г) 1/4
Д) 3/4
25. У султана было 10 визирей. Каждый визирь должен был ежегодно заплатить в казну налог – 1000 монет. Налог сдается в больших мешках с вензелем его владельца. Один из визирей хитрит – его монеты весят 19 граммов, тогда как у честных визирей монеты имеют вес 20 граммов. Какое минимальное количество взвешиваний необходимо сделать придворному судье на цифровых весах, чтобы уличить нечестного визиря? Можно взвешивать монеты, извлекая их из мешков.
А) 1
Б) 4
В) 5
Г) 9
Д) 10
26. Какие два числа являются логическим продолжением ряда 2, 5, 6, 11, 13, 14?
А) 20, 21
Б) 23, 24
В) 23, 27
Г) 24, 25
Д) 24, 27
27. Два графа 1 G и 2 G называются изоморфными, если между множествами их вершин можно установить соответствие, при котором сохраняется отношение смежности (две вершины называются смежными, если они соединены ребром).
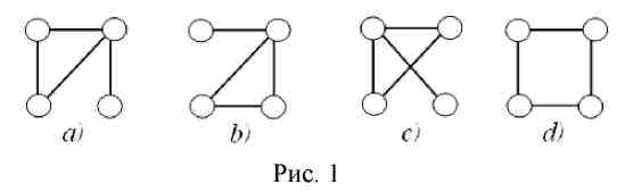
Например, на рис.1 изоморфными будут только графы a) и b), т.к. между их вершинами можно установить соответствие так, что каждому ребру в графе a) будет соответствовать ребро в графе b). Для остальных графов такого соответствия установить нельзя.
Для графов, приведенных на рисунке ниже, верно утверждение…
Для графов, приведенных на рисунке ниже, верно утверждение…
А) графы a) и b) изоморфны
Б) графы a) и c) изоморфны
В) графы b) и c) изоморфны
Г) все графы изоморфны друг другу
Д) все графы не изоморфны друг другу
28.Сколько существует способов составить слово «программист», если от каждой буквы диаграммы можно двигаться вниз или вправо?А) 10
Б) 11
В) 110
Г) 1024
Д) 2048
29. Автосалон продает три модели «Жигулей»: 2105, 2109 и 2110. Каждая из трех моделей может быть дооснащена любым количеством из четырех дополнительных опций (подогрев сидений, подогрев зеркал, подогрев руля и турбонаддув двигателя) или не оснащаться дополнительным оборудованием вовсе. Для каждой модели автомобиля и каждого набора опций выпускается прайс-лист. Один прайс-лист содержит базовую часть, содержащую информацию об одной модели «Жигулей» и дополнительную часть с каким-то набором опций. Тираж каждого прайс-листа практически неограничен и достаточен при любом наплыве посетителей. Посетителями салона являются только семейные пары. Муж и жена берут по одному прайс-листу по следующему правилу: базовая часть прайс-листов одинакова (семья заранее знает, какую модель «Жигулей» собирается купить), а дополнительная часть прайс-листов различна. В результате все семейные пары покидают салон, ничего не купив, но унося по паре прайс-листов. Чему равно наибольшее возможное количество семей, у которых пары прайс-листов различны?
А) 360
Б) 720
В) 12
Г) 384
Д) 768
30. Приведен фрагмент программы, реализованный на двух языках программирования. Предполагается, что начальное значение всех элементов массива а равно нулю.
Если n = 100, то sum принимает значение…
А) 5050
Б) 171700
В) 338350
Г) 10000
Д) 333300